Bayesian Independent Component Analysis

Out:

2

# Author: Pierre Ablin <pierre.ablin@ens.fr>
#
# License: MIT

import torch
from ksddescent import ksdd_lbfgs
from ksddescent.contenders import svgd
import matplotlib.pyplot as plt
import numpy as np


def amari_distance(W, A):
    """
    Computes the Amari distance between two matrices W and A.
    It cancels when WA is a permutation and scale matrix.
    Parameters
    ----------
    W : ndarray, shape (n_features, n_features)
        Input matrix
    A : ndarray, shape (n_features, n_features)
        Input matrix
    Returns
    -------
    d : float
        The Amari distance
    """
    P = np.dot(W, A)

    def s(r):
        return np.sum(np.sum(r ** 2, axis=1) / np.max(r ** 2, axis=1) - 1)

    return (s(np.abs(P)) + s(np.abs(P.T))) / (2 * P.shape[0])


def one_expe(n, p, sigma, bw, n_samples):
    W = sigma * np.random.randn(p, p)
    A = np.linalg.pinv(W)
    S = np.random.laplace(size=(p, n))
    X = np.dot(A, S)
    X = torch.tensor(X, dtype=torch.float)

    def score(w):
        N, _ = w.shape
        w_list = w.reshape(N, p, p)
        z = w_list.matmul(X)
        psi = torch.tanh(z).matmul(X.t()) / n - torch.inverse(
            w_list
        ).transpose(-1, -2)
        sc = -psi - w_list / sigma
        return sc.reshape(N, p ** 2)

    x = torch.randn(n_samples, p ** 2)
    x_final = ksdd_lbfgs(x.clone(), score, bw=bw)
    x_svgd = svgd(x.clone(), score, 0.1, bw=bw, max_iter=3000)
    score_svgd = torch.norm(score(x_svgd)).item()
    score_final = torch.norm(score(x_final)).item()
    score_random = torch.norm(score(x)).item()
    w_list = (x_final.reshape(n_samples, p, p)).detach().numpy()
    w_svgd = (x_svgd.reshape(n_samples, p, p)).detach().numpy()

    amari_ksd = np.sort([amari_distance(w, A) for w in w_list])
    amari_svgd = np.sort([amari_distance(w, A) for w in w_svgd])
    amari_random = np.sort(
        [amari_distance(np.random.randn(p, p), A) for w in w_svgd]
    )
    return (
        amari_ksd,
        amari_svgd,
        amari_random,
        score_final,
        score_svgd,
        score_random,
    )


p_list = [2]
n = 1000
sigma = 1
bw = 0.1
n_samples = 10

n_tries = 3
d_save = {}
for p in p_list:
    print(p)
    d_save[p] = {}
    amari_ksds = []
    amari_svgds = []
    amari_randoms = []
    score_ksds = []
    score_svgds = []
    score_randoms = []
    for i in range(n_tries):
        (
            amari_ksd,
            amari_svgd,
            amari_random,
            score_ksd,
            score_svgd,
            score_random,
        ) = one_expe(n, p, sigma, bw, n_samples)
        amari_ksds.append(amari_ksd)
        amari_svgds.append(amari_svgd)
        amari_randoms.append(amari_random)
        score_ksds.append(score_ksd)
        score_svgds.append(score_svgd)
        score_randoms.append(score_random)

plt.figure()
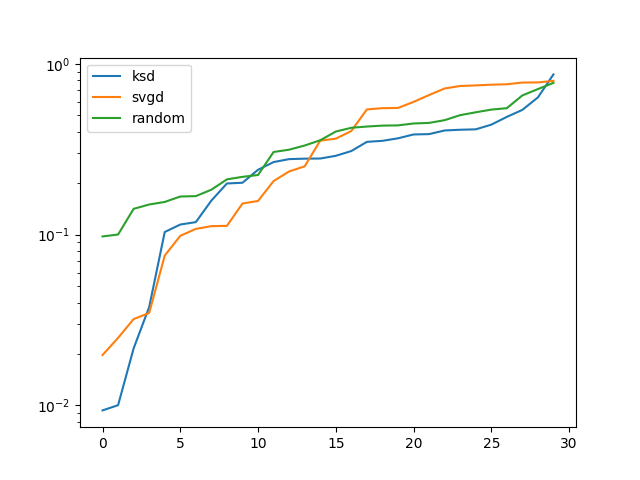
plt.plot(np.sort(np.ravel(amari_ksds)), label="ksd")
plt.plot(np.sort(np.ravel(amari_svgds)), label="svgd")
plt.plot(np.sort(np.ravel(amari_randoms)), label="random")
plt.yscale("log")
plt.legend()
plt.show()